Inhalt
Didaktische Bemerkungen
Demonstration 1  Reaktionswärme der Holzkohle bestimmen 
Demonstration 2  Lösungswärmen der Salze bestimmen
Demonstration 3  Bildungswärme bei der Reaktion von Eisen und Schwefel bestimmen
Ausblick  

Didaktische Bemerkungen

Chemische Reaktionen sind stets mit einem Energieumsatz verbunden. Diese Erfahrung entspricht auch den Alltagserfahrungen, beispielsweise beim Verbrennen von Heizöl oder von Holzkohle. Eine Hinführung zu diesem Thema erfolgte im Unterricht zuvor bei verschiedenen Experimenten („Kupfer und Schwefel“), bei den Schülerübungen oder bei den Sulfid-Reaktionen. Es soll nun demonstriert werden, dass die frei werdende Reaktionswärme nicht nur qualitativ wahrgenommen, sondern auch quantitativ gemessen und berechnet werden kann.
 
 
 
Zunächst wiegt man ein Holzkohlestückchen mit maximal 0,3 Gramm auf einer Waage ab und bestimmt die Masse auf zwei Stellen hinter dem Komma genau. Danach wird ein Kalorimeter in ein Stativ gespannt und mit der erforderlichen Menge destilliertes Wasser gefüllt (meist 0,5 Liter). Die genaue Masse des Wassers kann mit einem Messzylinder oder mit einer Waage bestimmt werden. Das Eingangsrohr unterhalb des Kalorimeters wird an eine mit Kalkwasser gefüllte Gaswaschflasche angeschlossen. Diese verbindet man mit der Sauerstoffflasche und stellt einen schwachen Gasstrom ein (etwa 2 bis 3 Blasen pro Sekunde).

Nun erfolgt eine genaue Messung der Wassertemperatur. Danach wird ein kleines Stück Holzkohle (maximal 0,3 Gramm!) mit der Tiegelzange über der nichtleuchtenden Brennerflamme an den Rändern zum Glühen gebracht und zügig in die Halterung des Kalorimeters eingesetzt. Der Kalorimeter sollte dann sofort verschlossen werden. Achtung: Die Sauerstoffzufuhr muss eventuell gedrosselt werden, vor allem wenn die Holzkohle zu stark aufglüht oder der Korken gar Feuer fängt!
 
Während des Verbrennens der Holzkohle wird der Rührstab gelegentlich auf und ab bewegt. Dies wird auch eine Weile nach dem vollständigen Verglühen des Kohlestückchens fortgesetzt. Danach liest man die Temperatur erneut ab und bestimmt die Temperaturdifferenz.
 
Beobachtung: Das glimmende Holzkohlestückchen glüht nach der Sauerstoffzufuhr hell auf. Gelegentlich beschlägt das Innere des Kalorimeters mit Wasserdampf. Die Verbrennung liefert Wärme, die das Wasser des Kalorimeters aufheizt. Die Temperaturzunahme kann an dem Thermometer abgelesen werden. Die Temperatur erreicht nach dem Ende der Verbrennung ihr Maximum.
 
Theorie: Bei der Verbrennung der Holzkohle wird Wärme frei, die das Wasser im Kalorimeter aufheizt. Die Reaktionsgleichung für die Verbrennung von Kohlenstoff lautet:
 
C  +  O₂   CO₂      ΔH_R = −393 kJ/mol
 
Die angegebene Reaktionswärme ΔH_R bezieht sich auf die Stoffmenge von 12 Gramm Kohlenstoff (1 Mol). Zunächst soll jedoch die absolute Wärmemenge Q berechnet werden. Die Berechnung erfolgt unter Einbeziehung der spezifischen Wärmekapazität (cP) des Wassers:

 
Q = cP (Wasser) × m (Wasser) × ΔT
 
Zur Erwärmung von 1 Gramm Wasser um 1 Kelvin (1° Celsius), sind (bei konstantem Druck) 4,19 Joule notwendig. Die Wärmekapazität des Kalorimeters soll hierbei vernachlässigt werden. Beispiel: Bei einer Messung erwärmen 0,3 Gramm Holzkohle 500 Gramm Wasser um 4,3 Kelvin oder 4,3 °C:
 
Q = 4,19 J/(g × K) × 500g × 4,3K = 9008,5 Joule
 
Bei der Verbrennung von 0,3 Gramm Holzkohle werden also 9008,5 Joule frei. Nun wird die Reaktionswärme bezogen auf die Stoffmenge des Kohlenstoffs berechnet. 0,3 Gramm Kohlenstoff entsprechen der Stoffmenge von 0,025 Mol. Die Reaktionswärme bei 1 Mol Kohlenstoff beträgt also:
 
ΔH_R = −9008,5 Joule/0,025mol = −360340 Joule/mol = −360,34 kJ/mol
 
Der errechnete Wert erhält ein negatives Vorzeichen, da bei der Reaktion Energie frei wird. Bei einem Vergleich mit dem theoretischen Wert (−393 kJ/mol) zeigt sich eine Abweichung, die durch bestimmte Faktoren verursacht werden kann: Die spezifische Wärmekapazität des Kalorimeters wurde nicht berücksichtigt. Bei der Verbrennung der Holzkohle wurde nicht nur das Wasser erwärmt, sondern auch das Glas und die umgebende Luft des Kalorimeters. Diese Wärmemenge floss nicht in das Wasser. Wird die Wärmekapazität der Kalorimeters mit berücksichtigt (200 J/g × K), erfolgt die Berechnung nach einer erweiterten Gleichung:

Q = 4,19 J/(g × K) × 500g × 4,3K + 200J/(g × K) × 4,3K = 9868,5 Joule

ΔH_R = −9868,5 Joule/0,025mol = −394740 Joule/mol = −394,74 kJ/mol

Die Holzkohle ist vielleicht mit Wasser oder mit Kohlenwasserstoffen verunreinigt. Der innere Beschlag im Kalorimeter deutet eventuell darauf hin. Beim Zünden des Holzkohle-Stückchens mit dem Brenner außerhalb des Kalorimeters geht bereits Wärme verloren. Die Abweichungen sollten diskutiert werden, weil durch sie das Prinzip der Messung von den Schülern besser verstanden wird.
 
 

Beim Lösen von Salzen in Wasser zerfallen die Ionenbindungen in Ionen, wobei ebenfalls Wärme abgegeben oder aufgenommen wird. Löst man das Salz Kaliumnitrat in Wasser, findet eine Abkühlung statt, da beim Lösungsvorgang Energie aus der Umgebung benötigt wird:
 
KNO₃   K⁺  +  NO₃⁻      ΔH_L = +36 kJ/mol
 
Andere Salze führen beim Lösen in Wasser zu einer Erwärmung, z.B. beim Natriumhydroxid:
 
NaOH   Na⁺  +  OH⁻      ΔH_L = −43 kJ/mol
 

In einer Schülerübung (>Arbeitsblatt) bestimmen die Schüler die absoluten Wärmemengen und die molaren Lösungswärmen selbst und vergleichen dann mit den theoretischen Werten (siehe auch Tabellen zu den Bildungsenthalpien der Ionen). Auch hier soll die spezifische Wärmekapazität der verwendeten Gefäße vernachlässigt werden.

 
Bei der exothermen Sulfid-Reaktion von Eisen und Schwefel wird viel Energie frei:
 
Fe  +  S   FeS     ΔH_B = −100 kJ/mol
 
7g Eisenpulver werden in einer Reibschale mit 4 Gramm Schwefel vermischt. Von dem Gemisch wiegt man auf einer Waage genau 8,8 Gramm ab und füllt es in ein kleineres Reagenzglas (16×180mm). Ein Becher aus dünnem, transparentem Kunststoff, der in einem zweiten steht, wird mit genau 250 Gramm (250ml) Wasser gefüllt. Der genaue Aufbau der Apparatur ist der Zeichnung zu entnehmen: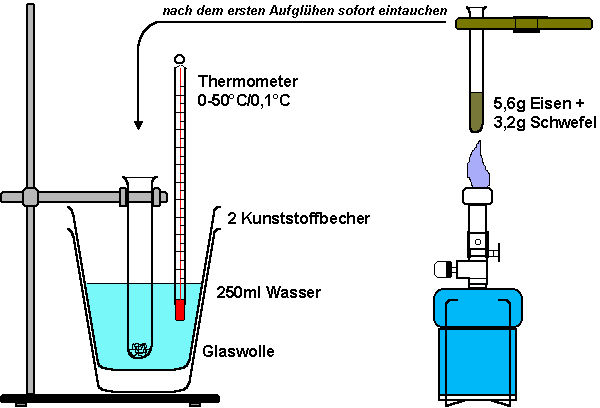
 

Am Boden des größeren Reagenzglases, welches in das Wasser taucht, befindet sich wenig Glaswolle. Die Wassertemperatur wird auf 0,1 °C genau gemessen. Danach erhitzt man das Gemisch im Reagenzglas mit der nicht leuchtenden Brennerflamme solange, bis es zu glühen beginnt. Das Reagenzglas wird möglichst rasch in das ins Wasser getauchte Reagenzglas hinein gestellt. Der Thermometer sollte während der Reaktion aus Sicherheitsgründen nicht in das Wasser gehalten werden. Nach Beendigung der Reaktion rührt man mit dem Thermometer vorsichtig um und liest danach die höchste, erreichbare Temperatur ab.
 
Beobachtungen: Das Eisen-Schwefel-Gemisch glüht hell auf, die Glut-Zone wandert durch das Gemisch. Dabei erwärmt sich das Wasser im Becher.
 
Theorie: Bei diesem Versuch entspricht die absolute Wärmemenge Q genau einem Zehntel der molaren Reaktionswärme ΔH_R, da 5,6 Gramm Eisen und 3,2 Gramm Schwefel (total =8,8 Gramm) genau 0,1 Mol der beteiligten Stoffe entsprechen:
 
Q = cP (Wasser) × m (Wasser) × ΔT
 
Berechnung eines Versuchs, bei dem sich das Wasser um 8,6 Kelvin (°C) erwärmt:
 
Q = 4,19 J/(g × K) × 250g × 8,6K = 9008,5 Joule
 
ΔH_B = −9008,5 Joule/0,1mol = −90085 Joule/mol = −90,085 kJ/mol

Aufgrund der exothermen Reaktion erhält die errechnete Bildungswärme ein negatives Vorzeichen. Der Vergleich mit dem theoretischen Wert (−100kJ/mol) zeigt eine Abweichung von etwa 10%. Auch hier erscheint eine Fehlerdiskussion sinnvoll:

• Beim Erhitzen des Reagenzglases mit dem Brenner wird dem System Energie zugeführt, die das Wasser später mit aufheizt. Diese Fehlerquelle müsste den Wert erhöhen.
• Da die Reaktion außerhalb des Messkalorimeters bereits beginnt, geht einiges an Wärme verloren.
• Die spezifische Wärmekapazität der Plastikbecher wird nicht berücksichtigt, auch dies erniedrigt den Wert, da dem System Wärme verloren geht.

ΔH_R  =  ∑ΔH_{B (Endstoffe)} − ∑ΔH_{B (Ausgangsstoffe)}

für die Reaktion Fe  +  S     FeS:
 
ΔH_R = −100kJ − (0 + 0) = −100 kJ/mol

Ausblick

Die Berechnung der Reaktionswärmen kann an weiteren Übungsbeispielen verdeutlicht werden. Die Messung von Neutralisationswärmen bei der Neutralisation von Natronlauge durch Schwefelsäure und die Bestimmung der Reaktionswärmen bei Redoxreaktionen, wenn man zum Beispiel Zinkpulver zu einer Kupfer(II)-sulfat-Lösung in einem Thermosbehälter gibt, dienen zur weiteren Vertiefung.